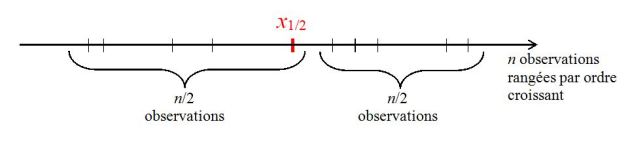
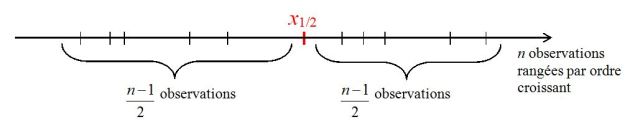
La médiane d'une série statistique
Première convention
Idée de base
Supposons que l'on ait réalisé
observations et qu'on les ait rangées par ordre croissant (série statistique ordonnée).
La première convention définit la médiane
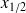comme étant l'observation qui, dans la série statistique ordonnée, occupe la (
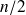)e position :
On dit encore que la médiane est l'observation de rang
.
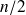Exemple : Série statistique avec un nombre pair d'observations
Soit la série statistique de taille
(
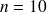est pair) suivante :
Pour rechercher la médiane de cette série, il faut avant toute chose ranger les observations par ordre croissant, c'est-à-dire considérer la série statistique ordonnée :
D'après la première convention, la médiane est l'observation occupant la 5e (
) position dans la série statistique ordonnée (on dit que la médiane est l'observation de rang 5) :
Exemple : Série statistique avec un nombre impair d'observations
Soit la série statistique de taille
(
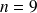est impair) suivante :
Pour rechercher la médiane de cette série, il faut commencer par ranger les observations par ordre croissant, c'est-à-dire considérer la série statistique ordonnée :
étant impair,
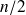n'est pas un nombre entier (
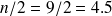) et il n'existe dès lors aucune observation de rang égal à
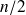. Comment définir alors la médiane ? On décide de prendre pour médiane l'observation de rang 5 :
.
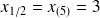Il est clair que cette petite adaptation de la définition initiale de la médiane n'altère en aucune façon le caractère « central » de cette dernière.
Remarquons que le rang de la médiane est égal à
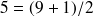, ou encore que
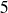est le plus petit entier supérieur ou égal à
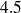(ce que l'on peut noter par
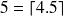; on dira encore que
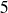est la valeur obtenue en arrondissant
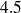à l'entier supérieur). On a donc
Remarque :
Si
est pair,
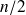est un nombre entier et
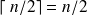. Ainsi, si
,
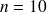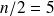et
.
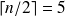Cette constatation permet d'unifier la définition de
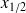quelle que soit la parité de
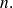Que
soit pair ou impair,
Définition : Première convention
Soit la série statistique
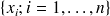, donnant lieu à la série statistique ordonnée
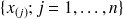. La médiane
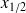de cette série est l'observation de rang
:
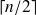En d'autres termes,
• si
est pair :
• si
est impair :
Seconde convention
Supposons à nouveau que l'on ait réalisé
observations et qu'on les ait rangées par ordre croissant (série statistique ordonnée).
La seconde convention définit la médiane
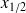comme étant une valeur occupant une position centrale dans la série statistique ordonnée, en ce sens que le nombre d'observations qui la précèdent est égal au nombre d'observations qui la suivent.
Exemple : Série statistique avec un nombre impair d'observations (suite)
Reprenons la série statistique ordonnée de taille
(
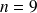est impair) suivante :
Selon la seconde convention, la médiane est l'observation occupant la 5e position dans la série ordonnée :
.
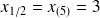En effet, le nombre d'observations qui la précèdent est bien égal au nombre d'observations qui la suivent (ce nombre est égal à
).
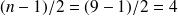On peut encore écrire que
Cet exemple nous montre aussi que, dans le cas d'une série statistique de taille impaire, les deux conventions conduisent à la même valeur pour la médiane.
Exemple : Série statistique avec un nombre pair d'observations (suite)
Reprenons la série statistique ordonnée de taille
(
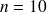est pair) suivante :
Puisque
est pair, aucune observation ne laisse autant d'observations avant elle qu'après elle
MAIS
toute valeur comprise entre
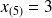et
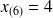laisse 5 observations avant elle et 5 observations après elle. On dit que
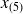et
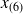définissent un intervalle médian.
L'usage d'un intervalle n'est pas aussi simple que celui d'une valeur. Aussi la convention veut-elle que l'on définisse la médiane comme la moyenne arithmétique des observations qui délimitent l'intervalle médian :
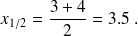
Remarquons encore que
Définition : Seconde convention
Soit la série statistique
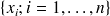, donnant lieu à la série statistique ordonnée
.
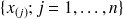Si
est impair :
Si
est pair :
Quelle convention choisir ?
Dans le cas où la taille
de la série statistique est impaire, les deux conventions conduisent à la même valeur pour la médiane. Dans le cas où la taille
de la série est paire, la médiane obtenue selon la première convention est généralement peu différente de la médiane calculée selon la seconde convention. L'utilisateur peut donc opter pour la convention avec laquelle il se sent le plus à l'aise, son choix n'ayant finalement que peu d'impact sur le résultat obtenu.
Même si la seconde convention est plus fréquemment utilisée par les statisticiens (les logiciels statistiques, par exemple, calculent généralement la médiane selon cette seconde convention ; c'est plus souvent cette seconde convention qui est présentée dans les manuels de statistique), la première convention présente des avantages certains :
elle est plus naturelle et plus facile à mettre en œuvre que la seconde convention, du moins dans le cas où
est pair ;contrairement à la seconde convention, elle fournit une médiane qui correspond toujours à une valeur observée, ce qui en rend l'interprétation plus naturelle ;
elle peut être mise en œuvre même si la variable observée est qualitative, pour autant qu'elle soit ordinale (alors que la seconde convention, si
est pair, n'est applicable que si la variable est quantitative) ;sa reformulation dans le cas d'une D.O.1 (voir ci-après) est identique à la convention utilisée pour définir la médiane d'une distribution de probabilités (cf. variables aléatoires discrètes).
Remarques sur la médiane
Remarque :
Tout comme la moyenne arithmétique
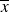, la médiane est une valeur unique.
Remarque :
Dans de nombreux cas (dans tous les cas, avec la première convention), la médiane est une valeur observée – contrairement à la moyenne
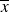– ce qui lui donne un sens concret évident.
Remarque :
Contrairement à la moyenne, la médiane est insensible à la présence d'une valeur extrême (ou aberrante).
Exemple :
Dès lors, en présence d'une valeur extrême (ou aberrante), le choix de la médiane comme valeur centrale est bien plus indiqué que celui de la moyenne arithmétique.
